caracteristicas de los números reales
Caracterización axiomática
Existen diferentes formas de construir el conjunto de los números reales a partir de axiomas, siendo la caracterización más común mediante las siguientes tres propiedades:
|
Las primeras dos condiciones definen el concepto de campo ordenado, mientras que la tercera propiedad es de naturaleza topológica y es la que diferencia al conjunto de los números reales de todos los demás campos ordenados. Hay que hacer notar que, en principio pueden existir diferentes conjuntos que satisfagan las mismas condiciones y que podrían ser diferentes al conjunto de los números reales, pero un teorema establece que si eso sucediera, ambas estructuras serían esencialmente la misma.
|
En vista de lo anterior podemos hablar de el conjunto de los números reales (y no de un conjunto de números reales) y estableciendo su unicidad se puede usar el símbolo para representarlo.
Al enunciar la tercera propiedad en ocasiones se especifica que es completo en el sentido de Dedekind, pues existen otros axiomas que se pueden usar y que, asumiendo las primeras dos condiciones, todos son lógicamente equivalentes. Algunos de estos son:
- (Cauchy) El conjunto K cumple que cualquier sucesión de Cauchy es convergente.
- (Bolzano-Weierstrass) El conjunto K cumple que cualquier sucesión acotada tiene una subsucesión convergente.
- Cualquier sucesión decreciente de intervalos cerrados tiene intersección no vacía.
Cada una de las primeras dos propiedades mencionadas al inicio de la sección corresponden a su vez a otra serie de axiomas, de modo que si se hace un desglose, puede caracterizarse el conjunto de los números reales como un conjunto que satisfaga la siguiente lista de axiomas.
- Si , entonces (Cerradura en la suma)
- Si , entonces (Conmutatividad en la suma)
- Si , entonces (Asociatividad en la suma)
- Existe de manera que para todo (Neutro aditivo)
- Para cada existe un elemento tal que (Inverso aditivo)
- Si , entonces (Cerradura en la multiplicación)
- Si , entonces (Conmutatividad en la multiplicación)
- Si , entonces (Asociatividad en la multiplicación)
- Existe de manera que para cualquier (Neutro multiplicativo)
- Para cada existe un elemento tal que (Inverso multiplicativo)
- Si , entonces (Distributividad de la multiplicación en la suma)
-
Si , entonces se cumple sólo una de estas: (Tricotomía)
- x<y
- y<x
- x=y
- Si , y entonces (Transitividad)
- Si y , entonces (Monotonía en la suma)
- Si , y , entonces (Monotonía en la multiplicación)
- Si es un conjunto no vacío acotado superiormente en , entonces tiene supremo en (Axioma del supremo)
Los axiomas del 1 al 15 corresponden a la estructura más general de cuerpo ordenado. El último axioma es el que distingue de otros cuerpos ordenados como .
Construcción por números decimales
Consideramos los números decimales como los conocemos intuitivamente. Sabemos que , es decir, el número π se expresa como elnúmero entero 3 y una secuencia infinita de dígitos 1, 4, 1, 5, 9, 2, etc.
Un número decimal se expresa entonces como donde es un número entero y cada es un elemento del conjunto . Además, consideramos que no existen las colas de 9.
Al conjunto de todos los números decimales donde es un número entero positivo se le denota por y se le llama el conjunto de los números reales positivos.
Al conjunto de todos los números decimales donde es un número entero negativo se le denota por y se le llama el conjunto de los números reales negativos.
Al número decimal se le llama cero.
Al conjunto se le denota por y se le llama conjunto de números reales.
Se define la relación de orden total de los números decimales como
-
 para todo
para todo 
-
 siempre que
siempre que  y
y 
-
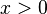 para todo
para todo 
-
Dados dos números reales cualesquiera
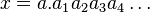 y
y  ,
,  en cualquiera de los casos siguientes:
en cualquiera de los casos siguientes:
- a>b
-
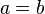 y además existe
y además existe  tal que
tal que  para todo
para todo  y
y 
Construcción por cortaduras de Dedekind
Hay valores que no se pueden expresar como números racionales, tal es el caso de  . Sin embargo es claro que se puede aproximar
. Sin embargo es claro que se puede aproximar  con números racionales tanto como se desee. Podemos entonces partir al conjunto de los números racionales en dos subconjuntos A y B de manera que en el conjunto A se encuentran todos los números racionales
con números racionales tanto como se desee. Podemos entonces partir al conjunto de los números racionales en dos subconjuntos A y B de manera que en el conjunto A se encuentran todos los números racionales  y en todos los números racionales tales que
y en todos los números racionales tales que  .
.
Una cortadura de dedekind es un par ordenado (A,B) que hace precisamente esto. Conceptualmente, la cortadura es el "espacio" que hay entre A y B. De esta manera es posible definir a como (A,B) tal que
como (A,B) tal que  y
y  .
.
Es posible demostrar que B queda unívocamente definido por A, de esta manera la cortadura se reduce simplemente a A.
También es demostrable que el conjunto de todas las cortaduras cumple con los axiomas de los números reales, de esta manera R es el conjunto de todas las cortaduras de Dedekind. Esta es la primera construcción formal de los números reales bajo la teoría de conjuntos.
Construcción por sucesiones de Cauchy
Las sucesiones de Cauchy retoman la idea de aproximar con números racionales un número real. Tómese por ejemplo, la ecuación.
Es claro que esta sumatoria opera sólo con los números racionales de la forma  , sin embargo el resultado final es el número irracional
, sin embargo el resultado final es el número irracional  . Cada vez que se añade un término, la expresión se aproxima más y más a
. Cada vez que se añade un término, la expresión se aproxima más y más a  .
.
Las sucesiones de Cauchy generalizan este concepto para definir a los números reales. Primero se define que una sucesión de números racionales es una función se denota simplemente por 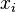 .
.
Una sucesión de Cauchy es una sucesión de números racionales donde sus elementos cada vez son menos diferentes. Más formalmente, se define como una sucesión de números racionales tales que para todo  existe un
existe un tal que para todo
tal que para todo  se cumple
se cumple  .
.
De esta manera es posible definir al número real  como la sucesión de números racionales:
como la sucesión de números racionales:



